The Twin Paradox
1. Intro
We implement in Sagemath manifolds the computations for the twin problem1 When a twin can undergo instantaneous changes in speed, Bondi’s \(k\)-calculus provides a simpler framework. as discussed in Chapter 2 of Gourgoulhon, Relativité restreinte.2 Or the English version: Gourgoulhon, Special Relativity in General Frames. We expect that the reader of the code 3 This link offers further examples for Sagemath and differential geometry. below has a copy of this book at hand. When referring to, for instance, equation (2.1) of this book, we write (G.2.1).
2. The space
We first need a 2D Minkowski space with coordinates \(t\) and \(x\).4
The Black python code formatter hangs on X.<c,t>. I therefore instantiate the chart slightly differently.
M = Manifold(2, 'M', structure='Lorentzian')
X = M.chart(names=("t", "x"))
t, x = X[:]
# X.<t,x> = M.chart() # the black formatter does not like this syntax
Next is the metric.
g = M.lorentzian_metric('g', signature='positive')
g[0, 0], g[1, 1] = -1, 1
show(g.disp())
show(g.signature())
\[ g = -\mathrm{d} t\otimes \mathrm{d} t+\mathrm{d} x\otimes \mathrm{d} x \] \[ 0 \]
3. The Curve
Here is the \(x\) coordinate of the path \(\mathscr{L}'\).
c, alpha, T = var('c alpha T', domain='positive')
x = c * T / alpha * (sqrt(1 + (alpha * t / T) ^ 2) - 1)
show(x)
\[ \frac{T c {\left(\sqrt{\frac{\alpha^{2} t^{2}}{T^{2}} + 1} - 1\right)}}{\alpha} \]
With this, we build the part of the path \(\mathscr{L}'\) from the point \(A\) at which the twins separate to the point \(C\) at which the twin that is flying hits the brakes to slow down; we skip the other three parts of \(\mathscr{L}'\).5 They follow from symmetry.
Lp = M.curve(
[c * t, x],
(t, 0, T / 4),
chart=X,
name='Lp',
)
show(Lp.display())
To plot \(\mathscr{L}'\) we need to choose numerical values for \(T\), \(\alpha\), and the speed of light \(c\). We achieve this by substituting the numerical values in \(x\), and then defining a new curve with these values.
x_of_t = x.subs({alpha: 8, T: 5, c: 1})
Lp_plot = M.curve(
(x_of_t, t),
(t, 0, 5 / 4),
)
p = Lp_plot.plot()
p.save("twins_curve.png", figsize=(3, 3), dpi=300)
The figure below shows the worldline of the twin that is undergoing the accelerations.6 The axis labels do not follow the convention of special relativity to have \(t\) pointing upward and \(x\) sideways. For the moment, I don’t know how to repair this.
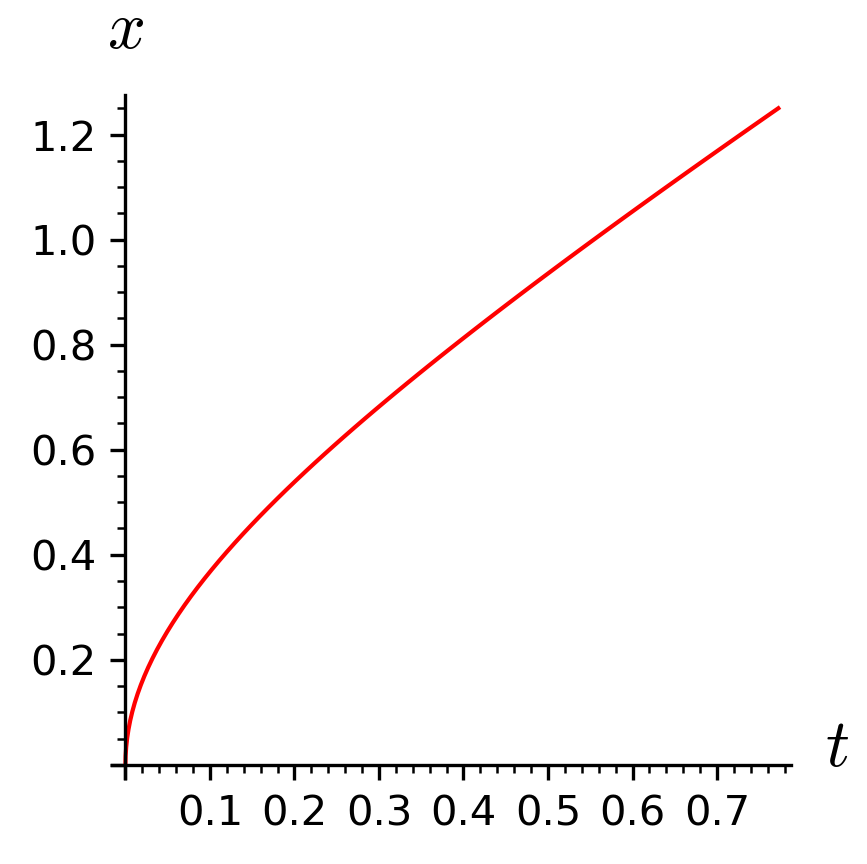
4. Proper time
For the infinitesimal proper time \(\d \tau\) we have from (G.2.9)
\begin{align*} c \d \tau = \sqrt{- g(\mathbf{v}, \mathbf{v})} \d t, \end{align*}where \(\mathbf{v}\) is a tangent vector of the path parametrized by \(t\). Thus, we need to compute the tangent vector \(\mathbf{v}\) first.
v = Lp.tangent_vector_field(name='v', latex_name='\\mathbf{v}')
show(v.display())
\[ \mathbf{v} = c \frac{\partial}{\partial t } + \left( \frac{\alpha c t}{\sqrt{\alpha^{2} t^{2} + T^{2}}} \right) \frac{\partial}{\partial x } \]
For the dot product \(\mathbf{v} \cdot \mathbf{v}\) we have to pullback the metric from \(M\) to \(\mathscr{L}'\).
d_tau = sqrt(-g.along(Lp)(v, v)) / c
show(d_tau.disp())
The proper time of the first quarter of the total curve from leaving to returning is \(\tau = \int_0^{T/4} \d \tau\):
Tp = integral(d_tau.expr(), t, 0, T / 4)
show(Tp/T)
\[ \frac{\operatorname{arsinh}\left(\frac{1}{4} \, \alpha\right)}{\alpha} \]
5. Four vectors
From \(\mathbf{v}\) we compute the \(4\)-velocity \(\mathbf{u} = \mathbf{v} /|| \mathbf{v} ||\).
u = v / v.norm(g.along(Lp))
show(u.disp())
\[ \left( \frac{\sqrt{\alpha^{2} t^{2} + T^{2}}}{T} \right) \frac{\partial}{\partial t } + \frac{\alpha t}{T} \frac{\partial}{\partial x } \]
Note that the next two ways of computing the norm are the same.
show(v.norm(g.along(Lp)) == sqrt(-g.along(Lp)(v, v)))
\[ \mathrm{True} \]
The \(4\)-acceleration is defined as
\begin{align*} \mathbf{a} = \frac{\d \mathbf{u}}{ c \d t'} = \frac{\d \mathbf{u}}{ \d t}\frac{\d t}{c \d t'}. \end{align*}We first compute \(\d \mathbf{u}/\d t\).
du_dt = Lp.tangent_vector_field(latex_name='\\d u/\\d t')
for i in M.irange():
du_dt[i] = diff(u[i].expr(), t)
show(du_dt.disp())
\[ \d u/\d t = \left( \frac{\alpha^{2} t}{\sqrt{\alpha^{2} t^{2} + T^{2}} T} \right) \frac{\partial}{\partial t } + \frac{\alpha}{T} \frac{\partial}{\partial x } \] The \(4\) acceleration now follows simply.
a = du_dt / (c * d_tau)
show(a.disp())
\[ \frac{\alpha^{2} t}{T^{2} c} \frac{\partial}{\partial t } + \left( \frac{\sqrt{\alpha^{2} t^{2} + T^{2}} \alpha}{T^{2} c} \right) \frac{\partial}{\partial x } \]
Here are some further checks: \(\mathbf{u}\cdot \mathbf{u}\) should equal \(-1\), and \(\mathbf{u}\cdot \mathbf{a} = 0\).
show(g.along(Lp)(u, u).disp())
show(g.along(Lp)(u, a).disp())
Finally, let’s check that \(\mathbf{a}\cdot \mathbf{a}\) corresponds to \(\alpha^2/c^{2} T^{2}\).
show(g.along(Lp)(a, a).disp())
6. Export to \(\LaTeX\)
This code facilitates the export to \(\LaTeX\).
def show(s):
s = latex(s).rstrip()
res = r"\[" # \begin{dmath*}"
res += "\n" + s + "\n"
res += r"\]" # end{dmath*}"
print(res)
