We have a project that consists of a number of jobs (tasks), and our customer likes to know the makespan, that is, how long it takes to complete the entire project. If we could do all jobs in parallel, then the makespan is just the processing time of the largest job. However, typically we cannot start some job when it depends on other jobs that have to be completed earlier. For instance, when building a house, we first need build the foundations, then the walls, the roof, electricity, and so on. When jobs have to respect such precedence relations, the computation of the makespan is not so simple anymore.

Assume that we did the boring work of computing the makespace, and we communicate this to our customer. As it happens, the customer likes to have the project completed a bit sooner. For this, we need to know what jobs form the critical path, that is, the critical jobs that constrain the makespan. Once we know the critical jobs, we might hire extra capacity (at extra cost) to reduce the time to process the job. Then we have to redo the boring makespan computation, inform the customer about the new makespan and the extra cost, and continue doing this for perhaps a few rounds. Clearly, we want to pass the computations of the makespan and the critical path on to the computer. And for this, we can again use memoization.

The procedure we develop below assumes that there no loops between jobs: if job \(2\) depends on the completion of job \(1\), then job \(1\) should not depend on the completion of job \(2\). Morever, we assume that jobs have positive processing time.

Before building the computer program, it helps to develop some mathematical notation; this acts as documentation at the same time. The earliest starting time of job \(i\) is defined as \(0\) when it has no predecessors, and otherwise as the completion times of its predecessors:

where we write \(j\to i\) to denote the set of predecessors of job \(i\). If \(j\to i\) is empty, then the maximum should default to the value 0. With this, the earliest completion time \(c_i\) of job \(i\) is its earliest starting time \(s_i\) plus its processing time \(p_i\), i.e,.

The makespan \(M\) of the project is evidently equal to the largest completion time of all jobs in the project \(P\), i.e.,

The latest starting time \(s_i'\) of job \(i\) is the latest time job can start without delaying the project. If we would know the latest completion time \(c_i'\) then

When job \(i\) has no successors, it must be that \(p_i' = M\), i.e., the makespan of the project. Otherwise,

where \(i\leftarrow j\) is the set of successors of job \(i\).

The critical path consists of all jobs without slack, that is, jobs whose earliest and latest completion time coincide.

The Job class follows the above notation nearly literally.

from functools import cache

class Job:
    def __init__(self, job_id, processing_time=0):
        self.job_id = job_id
        self.processing_time = processing_time
        self.predecessors = set()
        self.successors = set()

    @cache
    def earliest_start(self):
        return max(
            [p.earliest_completion() for p in self.predecessors], default=0
        )

    @cache
    def earliest_completion(self):
        return self.earliest_start() + self.processing_time

    @cache
    def latest_completion(self):
        return min(
            [p.latest_start() for p in self.successors],
            default=self.earliest_completion(),
        )

    @cache
    def latest_start(self):
        return self.latest_completion() - self.processing_time

    def clear(self):
        self.earliest_start.cache_clear()
        self.earliest_completion.cache_clear()
        self.latest_completion.cache_clear()
        self.latest_start.cache_clear()

Note that the computation of earliest start, and all other variables, is entirely implicit because we can rely on recursion to carry out the computations in the correct order, and on memoization to store the result. Next note that we actually don’t have to cache the earliest start and latest completion times because these functions are not called by other job instances. However, storing this extra information doesn’t hurt for any project that has a `human scale’, i.e., less than millions of jobs.

The Project class is conceptually just as simple as the Job class. We store the jobs in a dict. In the example below we provide the job processing times in a list, and the successors as a list of list.

class Project:
    def __init__(self):
        self.jobs = {}

    def add_job(self, job_id, time):
        self.jobs[job_id] = Job(job_id, processing_time=time)
        self.clear()

    def clear(self):
        self.makespan.cache_clear()
        for job in self.jobs.values():
            job.clear()

    def add_jobs(self, processing_times):
        for job_id, time in enumerate(processing_times):
            self.add_job(job_id, time)

    def make_graph(self, successors):
        for i, succ_list in enumerate(successors):
            job = self.jobs[i]
            for s in succ_list:
                successor = self.jobs[s]
                job.successors.add(successor)
                self.jobs[s].predecessors.add(job)

    @cache
    def makespan(self):
        return max(j.earliest_completion() for j in self.jobs.values())

    def critical_path(self):
        cp = []
        for job in self.jobs.values():
            if job.earliest_start() == job.latest_start():
                cp.append(job.job_id)
        return cp

To see how to the above works let’s consider an example project graph in Fig. 1 from Chapter 4 of a book of Michal Pinedo on scheduling.

digraph foo{
    rankdir=LR;
    size="5.3,9.7!";
   "0" -> "1";
   "1" -> "2" [ label = "5" ];
   "2" -> "4" [ label = "6" ];
   "4" -> "7" [ label = "12" ];
   "7" -> "10" [ label = "10" ];
   "10" -> "12" [ label = "9" ];
   "12" -> "14" [ label = "8" ];
   "1" -> "3" [ label = "5" ];
   "3" -> "6" [ label = "9" ];
   "3" -> "5" [ label = "9" ];
   "6" -> "9" [ label = "12" ];
   "6" -> "8" [ label = "12" ];
   "5" -> "9" [ label = "7" ];
   "5" -> "8" [ label = "7" ];
   "9" -> "11" [ label = "10" ];
   "8" -> "11" [ label = "6" ];
   "11" -> "12" [ label = "7" ];
   "11" -> "13" [ label = "7" ];
   "13" -> "14" [ label = "7" ];
   "14" -> "End" [ label = "5" ];
}

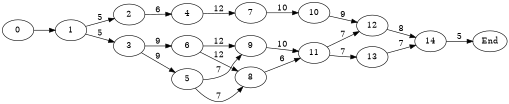
After converting the data from the above graph into lists, it remains to instantiate a project, and call the relevant functions.

process_times = [0, 5, 6, 9, 12, 7, 12, 10, 6, 10, 9, 7, 8, 7, 5]
successors = [
    [1],
    [2, 3],
    [4],
    [6, 5],
    [7],
    [8, 9],
    [8, 9],
    [10],
    [11],
    [11],
    [12],
    [12, 13],
    [14],
]

project = Project()
project.add_jobs(process_times)
project.make_graph(successors)

Let’s see what the makespan is.

print(project.makespan())

56

And here is the critical path.

print(project.critical_path())

[0, 1, 3, 6, 9, 11, 12, 13, 14]

With this tool, I am not afraid to negotiate with a customer.

There are (at least) two other ways to the find the critical path. One is with linear programming, the other with topological sorting. Consult the web if you’re interested.

Finally, you should note that the method to compute the critical path of a project is nearly identical to how to find the shortest path in a graph from a starting node to a finish node. With memoization shortest path computations become straightforward too.